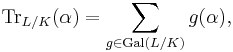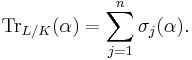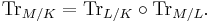Field trace
In mathematics, the field trace is a function defined with respect to a finite field extension L/K. It is a K-linear map from L to K. As an example, if L/K is a Galois extension and α is in L, then the trace of α is the sum of all the Galois conjugates of α, i.e.
where Gal(L/K) denotes the Galois group of L/K.
For a general finite extension L/K, the trace of an element α can be defined as the trace of the K-linear map "multiplication by α", that is, the map from L to itself sending x to αx. If L/K is inseparable, then the trace map is identically 0.
When L/K is separable, a formula similar to the Galois case above can be obtained. If σ1, ..., σn are the distinct K-linear field embeddings of L into an algebraically closed field F containing K (where n is the degree of the extension L/K), then
Properties of the trace
As mentioned above, the trace TrL/K : L → K is a K-linear map. Additionally, it behaves well in towers of fields: if M is a finite extension of L, then the trace from M to K is just the composition of the trace from M to L with the trace from L to K, i.e.
When L/K is separable, the trace provides a duality theory via the trace form: the map from L × L to K sending (x, y) to TrL/K(xy) is a nondegenerate, symmetric, bilinear form called the trace form. An example of where this is used is in algebraic number theory in the theory of the different ideal.
See also
References
- Section VI.5 of Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR1878556
- Roman, Steven (2006), Field theory, Graduate Texts in Mathematics, 158 (Second ed.), Springer, Chapter 8, ISBN 978-0-387-27677-9